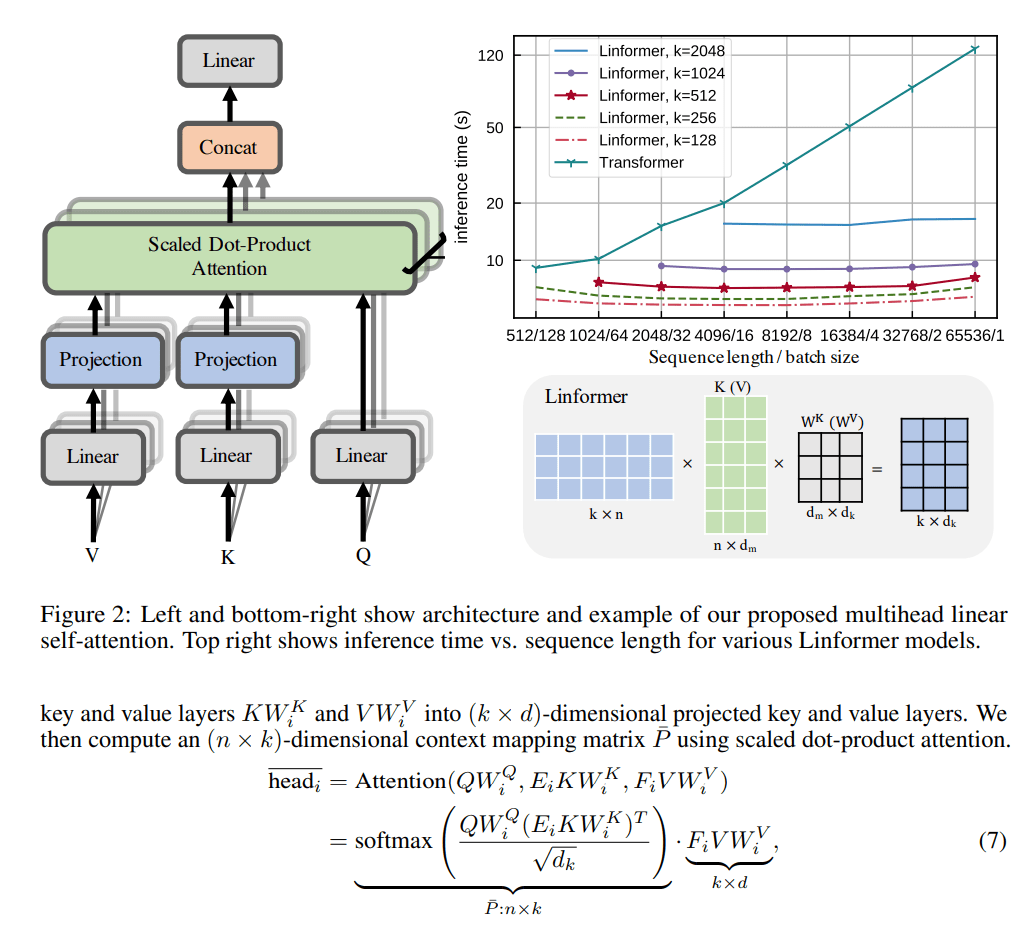
Linformer – make transformer affordable via low rank projection

transformer has been commonly used in recommendation system and it is the key building block to model sequence. however, transformer is very expensive. the computational cost of transformer is n^2 * d + n * d^2, where n represents the sequence length, for social media platform, it is easy build a sequence with potentially hundreds of actions, so a sequence of length 1K immediately will turn into a 1M operations.

Where this 1M comes from is during the self attention when calculating the attention scores QK_t.

Q: n * d, K: n * d => Q @ K_t = (n * d) @ (n * d)T = n ^ 2.

To avoid this from happening, researchers found that matrix are low rank matrices, which means by dimension reduction, we can project these matrices smaller matrices that will have a fixed dimension of r instead of n.

def linformer_attention(Q, K, V, E_K, E_V):
# Q: (n, d_k)
# K, V: (n, d_k)
# E_K, E_V: (n, r)
K_proj = E_K.T @ K # (r, d_k)
V_proj = E_V.T @ V # (r, d_k)

scores = (Q @ K_proj.T) / sqrt(d_k) # (n, r)
attn = softmax(scores, dim=-1) # (n, r)

out = attn @ V_proj # (n, d_k)
return out

In this psuedo code, we notice the attention score matrix is now n by r that grow linear with the sequence. In the very end, when we multiple with the value matrix, the dimension of r cancels out and we keep the final output exactly the same as the vanilla matrix. If we pick r to be 100 when n = 1000, using linformer will reduce the computation complexity by 10x.