Wikipedia listed several interesting properties for adjacency matrix powers:
Matrix powers[edit]
If A is the adjacency matrix of the directed or undirected graph G, then the matrix An (i.e., the matrix product of n copies of A) has an interesting interpretation: the element (i, j) gives the number of (directed or undirected) walks of length n from vertex i to vertex j. If n is the smallest nonnegative integer, such that for some i, j, the element (i, j) of An is positive, then n is the distance between vertex i and vertex j. A great example of how this is useful is in counting the number of triangles in an undirected graph G, which is exactly the trace of A3 divided by 6. We divide by 6 to compensate for the overcounting of each triangle (3! = 6 times). The adjacency matrix can be used to determine whether or not the graph is connected.
https://en.wikipedia.org/wiki/Adjacency_matrix#Matrix_powers
So, let’s use a simple example to demonstrate:
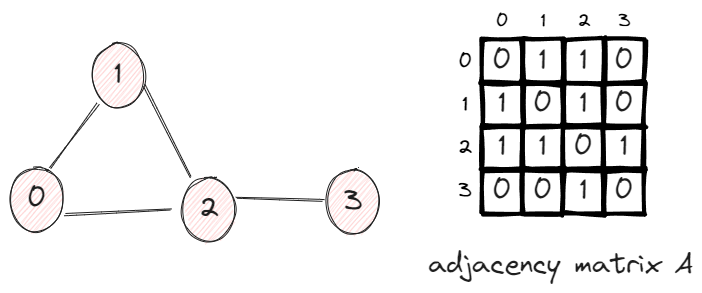
In this graph, we have 4 vertices and 4 edges. The adjacency matrix A has the value Aij = 1 if two vertices are connected, otherwise 0.
Walks of length n
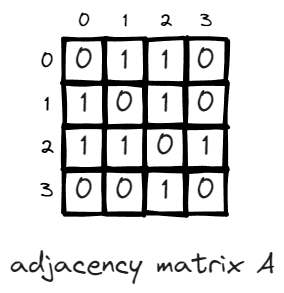
n = 1 is the first scenario, there is one walk between two nodes if they are connected, this is essentially the definition of adjacency matrix.
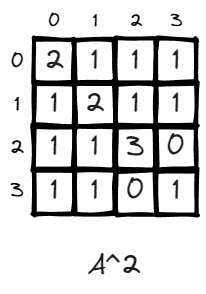
n = 2, the value of matrix changed, some values go up like (v2,v2) changed from 0 to 3. This is very intuitive. It means there doesn’t exist a path to walk from v2 back to v2 in one step, and there exit 3 paths if given two steps. (2>1>2, 2>2>2, 2>3>2).
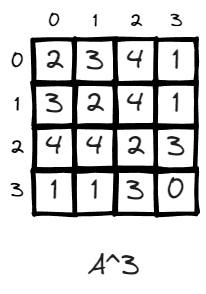
n = 3, (v2, v2) now becomes 2, it means there exist 2 paths to leave v2 and return to v2 in 3 steps, which is 2>1>3>2, 2>3>1>2.
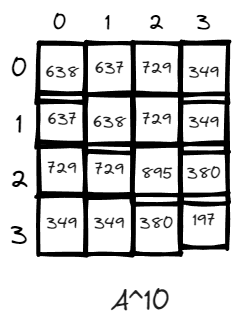
n = 10, just for fun, there exists many more paths when the power is high. V3 has the lowest number of paths likely due to it is a dead end within only one edges connecting it to the rest of the world via v2. And v2 has the highest number of returning to it self because it has the highest degree and is the central node of the graph.
In fact, the matrix multiplication is an exhausted approach to iterate through all the possible permutations of paths, for a unweighted graph, if a path exists, the value of all the edges of that path will be 1 and multiplication of these paths will be 1.
The matrix multiplication approach is basically a breath first tree search
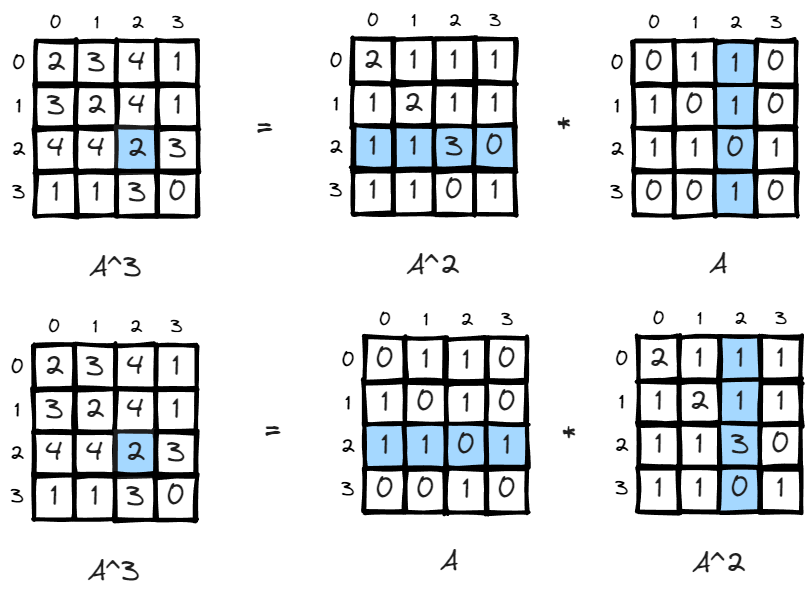
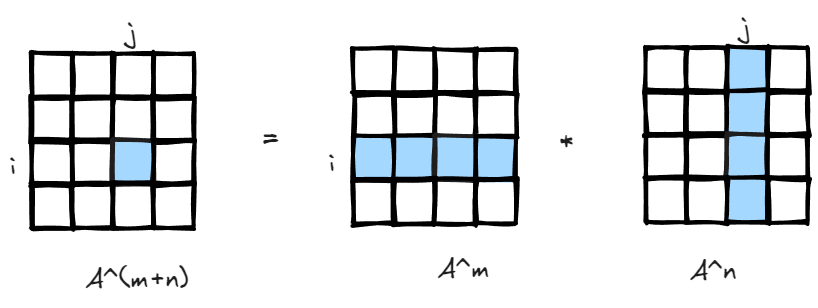
Since matrix multiplication is association, (A*B)*C=A*(B*C), the interpretation is also easy to understand, if there is a matrix storing how many paths there are leaving i to all other nodes in m steps, and another matrix storing all paths returning to j from all other nodes in n steps, you got the total number of paths leaving i return to j in m+n steps.
n being distance if it is first time An(i,j)>0
This is less straightforward, and the previous example of 4 vertices is not a good example to demonstrate this property because everything is so close to each other, so I added another node v4.
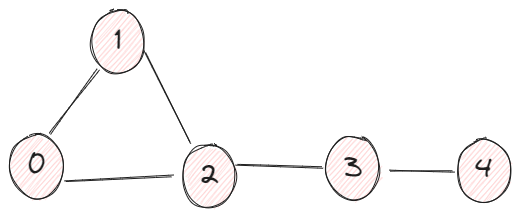
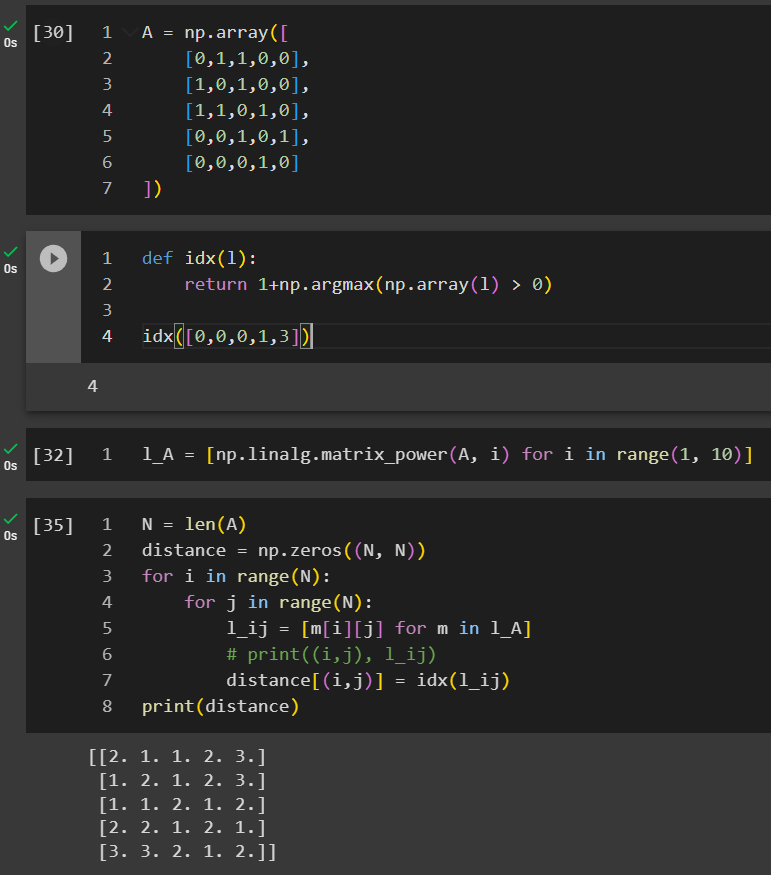
In this example, we created a list of l_A where it stored all the matrices when n increases from 1 to 9. We are looping through all the cells to identify under which n that An_ij first time becomes positive.
In conclusion, adjacency matrix has such interesting properties and it is symbolically simple, however, it is full permutation under the hood and likely won’t scale well to large graphs, so better algorithms or optimization is required given your application.